
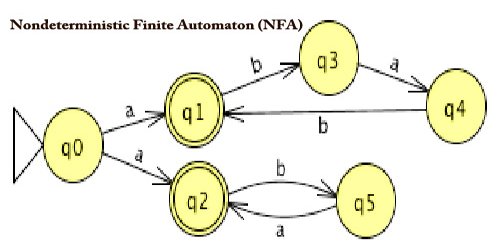
The only state it can accept in is state S1. It might appear to accept any binary value, but this isn't true. This means that the following inputs are valid: Once in S2 an input of 1 will keep it there, and an input of 0 will switch it back to S1. Looking at the above diagram we can see that it starts in state S1, an input of 1 will keep it in state S1, and an input of 0 will move it to state S2. Mainly engineering, biology and most commonly in linguistics, where they are used to describe languages.Ī finite state automata accepting binary input This is because the design clearly shows that it is impossible to transition from the state 'moving up' to the state 'moving down'.Īpplications of finite state machines are found in many sciences. Consider the example of the elevator: by modelling the system as a finite state machine, it is possible to show that the elevator is not able to move up and down without stopping. We can prove that the system is robust and will not behave in any unexpected manner.
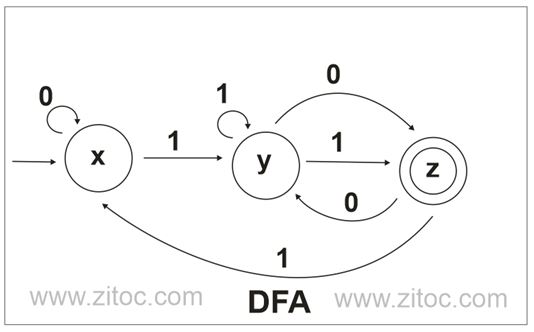
Representing a system as a finite state machine is very powerful because the model allows us to demonstrate the behaviour very clearly. We can also produce a state transition table (DEFINE THIS LANGUAGE BOX?):

from 'moving down' to 'static on floor 1' triggered by 'arrival 1'įorm the above we can draw the finite state machine for the elevator.from static on floor 2 to 'moving down' triggered by 'down button'.from 'moving up' to 'static on floor 2' triggered by 'arrival 2'.from 'static on floor 1' to 'moving up' triggered by 'up button'.'static on floor 1', 'moving up', 'static on floor 2', 'moving down' It models the behaviour of a system by showing each state it can be in and the transitions between each state. Finite state machines Ī finite state machine is a form of abstraction (WHY/HOW?).


 0 kommentar(er)
0 kommentar(er)
